- Коммутативная группа
-
Абелева или коммутативная группа есть группа, в которой групповая операция является коммутативной; то есть группа G абелева если ab = ba для любых двух элементов
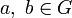 .
.Групповая операция в абелевых группах обычно называется «сложением» и обозначается знаком + .
Название дано в честь норвежского математика Абеля за его вклад в исследование групп подстановок.
Содержание
Примеры
- Группа параллельных переносов в линейном пространстве.
- Любая циклическая группа
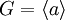 . Действительно, для любых x = an и y = am верно, что
. Действительно, для любых x = an и y = am верно, что
- xy = aman = am + n = anam = yx.
- В частности, целые числа
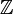 образуют коммутативную группу по сложению, также как и классы вычетов
образуют коммутативную группу по сложению, также как и классы вычетов 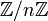 .
.
- Любое кольцо является коммутативной (абелевой) группой по своему сложению. В том числе и вещественные числа с операцией сложения.
- Обратимые элементы коммутативного кольца, в частности, ненулевые элементы любого поля, образуют абелеву группу по умножению. Например, вещественные числа, не равные нулю, с операцией умножения.
Связанные определения
- По аналогии с размерностью у векторных пространств, каждая абелева группа имеет ранг. Он определяется как минимальная размерность пространства над полем рациональных чисел, в которое вкладывается фактор группы по её кручению.
Свойства
- Конечнопорождённые абелевы группы изоморфны прямым суммам циклических групп.
- Конечные абелевы группы изоморфны прямым суммам конечных циклических групп.
- Любая абелева группа имеет естественную структуру модуля над кольцом целых чисел. Действительно, пусть n — натуральное число, а x — элемент коммутативной группы G с операцией, обозначаемой +, тогда nx можно определить как
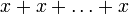 (n раз) и ( − n)x = − (nx).
(n раз) и ( − n)x = − (nx).
- Утверждения и теоремы, верные для абелевых групп (то есть модулей над кольцом главных идеалов
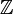 ), зачастую могут быть обобщены на модули над произвольным кольцом главных идеалов. Типичным примером является классификация конечнопорожденных абелевых групп.
), зачастую могут быть обобщены на модули над произвольным кольцом главных идеалов. Типичным примером является классификация конечнопорожденных абелевых групп.
- Утверждения и теоремы, верные для абелевых групп (то есть модулей над кольцом главных идеалов
- Множество гомоморфизмов
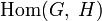 всех групповых гомоморфизмов из G в H само является абелевой группой. Действительно, пусть
всех групповых гомоморфизмов из G в H само является абелевой группой. Действительно, пусть 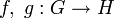 — два гомоморфизма групп между абелевыми группами, тогда их сумма f + g, заданная как (f + g)(x) = f(x) + g(x), тоже является гомоморфизмом (это неверно, если H некоммутативная группа).
— два гомоморфизма групп между абелевыми группами, тогда их сумма f + g, заданная как (f + g)(x) = f(x) + g(x), тоже является гомоморфизмом (это неверно, если H некоммутативная группа).
Конечные абелевы группы
Основополагающая теорема о структуре конечной абелевой группы утверждает, что любая конечная абелева группа может быть разложена в прямую сумму своих циклических подгрупп, порядки которых являются степенями простых чисел. Это следствие общей теоремы о структуре конечнопорождённых абелевых групп для случая, когда группа не имеет элементов бесконечного порядка.
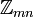 изоморфно прямой сумме
изоморфно прямой сумме 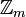 и
и 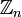 тогда и только тогда, когда m и n взаимно просты.
тогда и только тогда, когда m и n взаимно просты.Следовательно, можно записать абелеву группу G в форме прямой суммы
двумя различными способами:
- Где числа
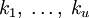 степени простых
степени простых - Где k1 делит k2, которое делит k3, и так далее до ku.
Например,
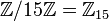 может быть разложено в прямую сумму двух циклических подгрупп порядков 3 и 5:
может быть разложено в прямую сумму двух циклических подгрупп порядков 3 и 5: 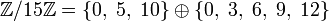 . То же можно сказать про любую абелеву группу порядка пятнадцать, приходим к выводу, что все абелевы группы порядка 15 изоморфны.
. То же можно сказать про любую абелеву группу порядка пятнадцать, приходим к выводу, что все абелевы группы порядка 15 изоморфны.Вариации и обобщения
- Дифференциальной группой называется абелева группа
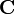 , в которой задан такой эндоморфизм
, в которой задан такой эндоморфизм 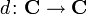 , что d2 = 0. Этот эндоморфизм называется дифференциалом. Элементы дифференциальных групп называются цепями, элементы ядра
, что d2 = 0. Этот эндоморфизм называется дифференциалом. Элементы дифференциальных групп называются цепями, элементы ядра 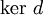 — циклами, элементы образа
— циклами, элементы образа 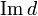 — границами.
— границами.
См. также
Литература
- Винберг Э. Б. Курс алгебры. — 3-е изд. — М.: Факториал Пресс, 2002. — 544 с. — 3000 экз. — ISBN 5-88688-060-7
Wikimedia Foundation. 2010.