- Алгоритм Полига-Хеллмана
-
Алгоритм Полига - Хеллмана (также называемый алгоритм Силвера — Полига — Хеллмана) — детерминированный алгоритм дискретного логирифмирования в кольце вычетов по модулю простого числа. Для модулей специального вида данный алгоритм является полиномиальным.
Содержание
История
Данный алгоритм был впервые описан американскими математиками Роланом Силвером (Roland Silver), Стефаном Полигом (Stephan Pohlig) и Мартином Хеллманом (Martin Hellman) в 1978 году в статье «An improved algorithm for computing logarithms over GF(p) and its cryptographic significance». Важной особенностью этого метода является то, что для простых чисел специального вида, можно находить дискретный логарифм за полиномиальное время.
Исходные данные
Пусть задано сравнение
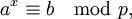
(1) и известно разложение p − 1на простые множители:
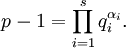
Необходимо найти натуральное число x, удовлетворяющее сравнению (1). Заметим, что на практике всегда рассматривается случай, когда a — первообразный корень по модулю p. В этом случае сравнение (1) имеет решение при любом b, взаимно простом с p.
Идея алгоритма
Суть алгоритма в том, что достаточно найти x по модулям
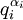 для всех i, а затем решение исходного сравнения можно найти с помощью китайской теореме об остатках. Чтобы найти x по каждому из таких модулей, нужно решить сравнение:
для всех i, а затем решение исходного сравнения можно найти с помощью китайской теореме об остатках. Чтобы найти x по каждому из таких модулей, нужно решить сравнение: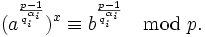
(2) Данное сравнение решается за полиномиальное время в случае, если qi — небольшое (то есть, не превосходит (logp)c, где c — некоторая константа).
Описание алгоритма
1 (составление таблицы). Составить таблицу значений {ri,j}, где
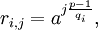
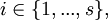
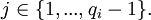
NB! i перебирает сами простые множители q1,q2(…,qs) а не 1..S а j может быть и нулем.
2 (нахождение
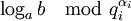 ).
Для i от 1 до s:
Пусть
).
Для i от 1 до s:
Пусть
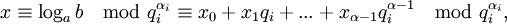 где
где
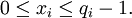 Тогда из (1) следует, что
Тогда из (1) следует, что
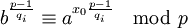 С помощью таблицы, составленной на шаге 1, находим x0.
Для j от 1 до α − 1
Рассматриваем сравнение
С помощью таблицы, составленной на шаге 1, находим x0.
Для j от 1 до α − 1
Рассматриваем сравнение
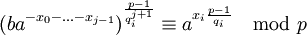 Решение опять же находится по таблице
Конец цикла по i
Конец цикла по j
3 (нахождение ответа). Найдя
Решение опять же находится по таблице
Конец цикла по i
Конец цикла по j
3 (нахождение ответа). Найдя 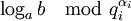 для всех i, находим
для всех i, находим 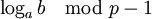 по китайской теореме об остатках.
по китайской теореме об остатках.
Сложность алгоритма
Решение сравнения (1) находится за
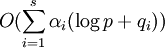 арифметических операций (см. [1]).
арифметических операций (см. [1]).Можно также сказать, что решение находится за
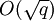 арифметических операций, где q — наибольший простой делитель p-1 (см. [3]).
арифметических операций, где q — наибольший простой делитель p-1 (см. [3]).Если все простые делители qi не превосходят
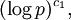 то алгоритм Полига-Хеллмана является полиномиальным и имеет сложность
то алгоритм Полига-Хеллмана является полиномиальным и имеет сложность 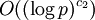 , где c1,2 — некоторые положительные постоянные.
, где c1,2 — некоторые положительные постоянные.Применение
Как уже было сказано, алгоритм Полига-Хеллмана крайне эффективен, если p-1 раскладывается на небольшие простые множители. Например, для чисел вида
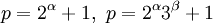 и т. д. Если же у p-1 есть большой простой делитель
и т. д. Если же у p-1 есть большой простой делитель 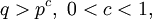 то алгоритм имеет экспоненциальную сложность. Это очень важно учитывать при выборе параметров криптографических схем.
то алгоритм имеет экспоненциальную сложность. Это очень важно учитывать при выборе параметров криптографических схем.Замечание
Для применения алгоритма Полига-Хеллмана необходимо знать разложение p-1 на множители. В общем случае задача факторизации — достаточно трудоёмкая, однако если делители числа — небольшие (в том смысле, о котором сказано выше), то это число можно быстро разложить на множители даже методом последовательного деления. Таким образом, в том случае, когда эффективен алгоритм Полига-Хеллмана, необходимость факторизации не усложняет задачу.
Литература
- Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. — Москва: МЦМНО, 2003. — С. 328. — ISBN 5-94057-103-4
- Pohlig S., Hellmann M. An improved algorithm for computing logarithms over GF(p) and its cryptographic significance. — IEEE Trans. Inform. Theory, V.5, 1978. — С. 106-110.
- Odlyzko A. M. Discrete logarithms in finite fields and their cryptographic significance // Advances in Crytology: Proceedings of EuroCrypt’84 /Thomas Beth, Norbert Cot, and Igemar Ingemarsson, editors. Berlin: Springer-Verlag, 1984 (Lect. Notes in Computer Science; V. 209). P. 224—316.
Wikimedia Foundation. 2010.
