Циклические коды

Циклический код — линейный код, обладающий свойством цикличности, то есть каждая циклическая перестановка кодового слова также является кодовым словом. Используется для преобразования информации для защиты её от ошибок (см. Обнаружение и исправление ошибок).

Введение

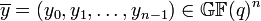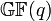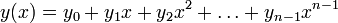Пусть $\overline{y} = ({y_0},{y_1},\dots,{y_{n-1}}) \in \mathbb{GF}(q)^n$ слово длины n над алфавитом из элементов конечного поля $\mathbb{GF}(q)$ и $y(x) = y_0 + y_1x + y_2x^2 +\dots+ y_{n-1}x^{n-1}$ полином, соответствующий этому слову, от формальной переменной x. Видно, что это соответствие не просто взаимнооднозначное, но и изоморфное. Так как «слова» состоят из букв из поля, то их можно складывать и умножать (поэлементно), причём результат будет в том же поле. 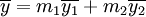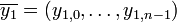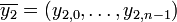Полином, соответствующий линейной комбинации $\overline{y} = m_1\overline{y_1} + m_2\overline{y_2}$ пары слов $\overline{y_1} = (y_{1,0},\dots,y_{1,n-1})$ и $\overline{y_2} = (y_{2,0},\dots,y_{2,n-1})$, равен линейной комбинации полиномов этих слов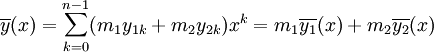 $\overline{y}(x) = \sum_{k=0}^{n-1} (m_1y_{1k} + m_2y_{2k} )x^k = m_1\overline{y_1}(x) + m_2\overline{y_2}(x)$

Это позволяет рассматривать множество слов длины n над конечным полем как линейное пространство полиномов со степенью не выше n-1 над полем $\mathbb{GF}(q)$

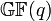
Алгебраическое описание

Если 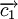$\overrightarrow{c_1}$ кодовое слово, получающееся циклическим сдвигом на один разряд вправо из слова 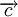$\overrightarrow{c}$, то ему соответствующий полином c₁(x) получается из предыдущего умножением на x:

$c_1(x) = xc(x)\mod(x^n-1)$, пользуясь тем, что $x^n \equiv 1 \mod(x^n-1)$,

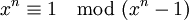Сдвиг вправо и влево соответственно на j разрядов:

$c_j(x) = x^jc(x)\mod(x^n-1)$

$c_{-j}(x)x^{j} = c(x)\mod(x^n-1)$

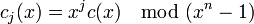
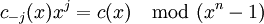
Если m(x) — произвольный полином над полем GF(q) и c(x) — кодовое слово циклического (n,k) кода, то m(x)c(x)mod(xⁿ − 1) тоже кодовое слово этого кода.

Порождающий полином

Определение Порождающим полиномом циклического (n,k) кода C называется такой ненулевой полином 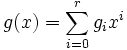$g(x)=\sum\limits_{i=0}^{r}g_ix^i$ из C, степень которого наименьшая и коэффициент при старшей степени g_r = 1.

Теорема 1

Если C — циклический (n,k) код и g(x) — его порождающий полином, тогда степень g(x) равна r = n − k и каждое кодовое слово может быть единственным образом представлено в виде

c(x) = m(x)g(x),

где степень m(x) меньше или равна k − 1.

Теорема 2

g(x) — порождающий полином циклического (n,k) кода является делителем двучлена xⁿ − 1

Следствия: таким образом в качестве порождающего полинома можно выбирать любой полином, делитель xⁿ − 1. Степень выбранного полинома будет определять количество проверочных символов r, число информационных символов k = n − r.

Порождающая матрица

Полиномы 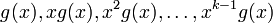$g(x), xg(x), x^2g(x),\dots,x^{k-1}g(x)$ линейно независимы, иначе m(x)g(x) = 0 при ненулевом m(x), что невозможно.

Значит кодовые слова можно записывать, как и для линейных кодов, следущим образом:

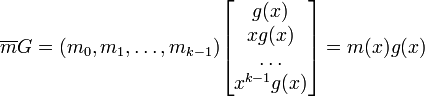$\overline{m}G=(m_0,m_1,\dots,m_{k-1}) \begin{bmatrix} g(x) \\ xg(x) \\ \dots \\ x^{k-1}g(x) \end{bmatrix} = m(x)g(x)$, где G является порождающей матрицей, m(x) — информационным полиномом.

Матрицу G можно записать в символьной форме: $G = \begin{bmatrix} g_0 & g_1 & \dots & g_{r-1} & g_r & 0 & \dots & 0 \\ 0 & g_0 & \dots & g_{r-2} & g_{r-1} & g_r & \dots & 0 \\ . & . & \dots & . & . & . & \dots & . \\ 0 & 0 & \dots & 0 & g_0 & g_1 & \dots & g_r \end{bmatrix}$

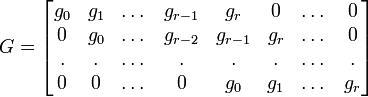
Проверочная матрица

Для каждого кодового слова циклического кода справедливо 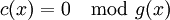$c(x) = 0\mod g(x)$. Поэтому проверочную матрицу можно записать как: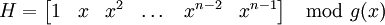

$H = \begin{bmatrix} 1 & x & x^2 & \dots & x^{n-2} & x^{n-1} \\ \end{bmatrix}\mod g(x)$

Тогда:

$\overline{c}H^T = \sum\limits_{i=0}^{n-1} c_ix^i = 0\mod g(x)$

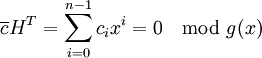
Кодирование

Несистематическое

При несистематическом кодирование кодовое слово получается в виде произведения информационного полинома на порождающий

c(x) = m(x)g(x).

Оно может быть реализовано при помощи перемножителей полиномов.

Систематическое

При систематическом кодировании кодовое слово формируется в виде информационного подблока и проверочного $c(x) = [s(x)\;m(x)]$

Пусть информационное слово образует старшие степени кодового слова, тогда

c(x) = x^rm(x) + s(x),r = n − k

Тогда из условия 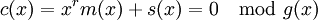$c(x)=x^rm(x) + s(x)=0\mod g(x)$, следует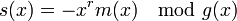

$s(x)=-x^r m(x)\mod g(x)$

Это уравнение и задает правило систематичекого кодирования. Оно может быть реализовано при помощи многотактных линейных фильтров(МЛФ)

Примеры

Двоичный (7,4,3) код

В качестве делителя x⁷ − 1 выберем порождающий полином третьей степени g(x) = x³ + x + 1, тогда полученный код будет иметь длину n = 7, число проверочных символов (степень порождающего полинома) r = 3, число информационных символов k = 4, минимальное расстояние d = 3.

Порождающая матрица кода:

$G = \begin{bmatrix} 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{bmatrix}$,

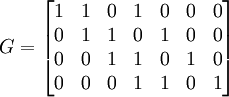где первая строка представляет собой запись полинома g(x) коэффициентами по возрастанию степени. Остальные строки — циклические сдвиги первой строки.

Проверочная матрица:

$H = \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 1 \end{bmatrix}$,

где i-ый столбец, начиная с 0-ого, представляет собой остаток от деления xⁱ на полином g(x), записанный по возрастанию степеней, начиная сверху.

Так, например, 3-ий столбец получается 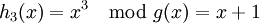$h_3(x)=x^3\mod g(x) = x+1$, или в векторной записи [110].

Легко убедиться, что GH^T = 0.

Двоичный (15,7,5) БЧХ код

В качестве порождающего полинома g(x) можно выбрать произведение двух делителей x¹⁵ − 1^

g(x) = g₁(x)g₂(x) = (x⁴ + x + 1)(x⁴ + x³ + x² + x + 1) = x⁸ + x⁷ + x⁶ + x⁴ + 1.

Тогда каждое кодовое слово можно получить с помощью произведения информационного полинома m(x) со степенью k − 1 таким образом:

c(x) = m(x)g(x).

Например, информационному слову $\overline m=[1000111]$ соответствует полином m(x) = x⁶ + x⁵ + x⁴ + 1, тогда кодовое слово c(x) = (x⁶ + x⁵ + x⁴ + 1)(x⁸ + x⁷ + x⁶ + x⁴ + 1) = x¹⁴ + x¹² + x⁹ + x⁷ + x⁵ + 1, или в векторном виде $\overline c=[1000010101001010]$

См. также

• Обнаружение и исправление ошибок
• Линейный код
• БЧХ код
• Конечное поле
• Многочлен над конечным полем

Ссылки

• Механизмы контроля целостности данных.