- Решето Аткина
-
В математике решето́ А́ткина — быстрый современный алгоритм нахождения всех простых чисел до заданного целого числа N. Основная идея алгоритма состоит в использовании неприводимых квадратичных форм (представление чисел в виде ax²+by²). Предыдущие алгоритмы в основном представляли собой различные модификации решета Эратосфена, где использовалось представление чисел в виде редуцированных форм (обычно произведения xy). Отдельный этап алгоритма вычеркивает числа, кратные квадратам простых чисел. Алгоритм был создан А. О. Л. Аткиным (англ.)русск. и Д. Ю. Бернштайном (англ.)русск. [1].
Содержание
Версия алгоритма на языке Pascal
program atkin; var is_prime:array[1..10001] of boolean; jj:int64; procedure dosieve(limit:int64); var i,k,x,y:int64; n:int64; begin for i:=5 to limit do is_prime[i]:=false; for x:=1 to trunc(sqrt(limit)) do for y:=1 to trunc(sqrt(limit)) do begin n:=4*sqr(x)+sqr(y); if (n<=limit) and ((n mod 12 = 1) or (n mod 12 = 5)) then is_prime[n]:=not is_prime[n]; n:=n-sqr(x); if (n<=limit) and (n mod 12 = 7) then is_prime[n]:=not is_prime[n]; n:=n-2*sqr(y); if (x>y) and (n<=limit) and (n mod 12 = 11) then is_prime[n]:=not is_prime[n]; end; for i:=5 to trunc(sqrt(limit)) do begin if is_prime[i] then begin k:=sqr(i); n:=k; while n<=limit do begin is_prime[n]:=false; n:=n+k; end; end; end; is_prime[2]:=true; is_prime[3]:=true; end; begin dosieve(10000); for jj:=1 to 10000 do if is_prime[jj] then writeln(jj); end.
Упрощённая версия алгоритма
Ниже представлена упрощённая версия кода на языке программирования C++, иллюстрирующая основную идею алгоритма — использование квадратичных форм[2].
int limit = 1000; int sqr_lim; bool is_prime[1001]; int x2, y2; int i, j; int n; // Инициализация решета sqr_lim = (int)sqrt((long double)limit); for (i = 0; i <= limit; i++) is_prime[i] = false; is_prime[2] = true; is_prime[3] = true; // Предположительно простые - это целые с нечетным числом // представлений в данных квадратных формах. // x2 и y2 - это квадраты i и j (оптимизация). x2 = 0; for (i = 1; i <= sqr_lim; i++) { x2 += 2 * i - 1; y2 = 0; for (j = 1; j <= sqr_lim; j++) { y2 += 2 * j - 1; n = 4 * x2 + y2; if ((n <= limit) && (n % 12 == 1 || n % 12 == 5)) is_prime[n] = !is_prime[n]; // n = 3 * x2 + y2; n -= x2; // Оптимизация if ((n <= limit) && (n % 12 == 7)) is_prime[n] = !is_prime[n]; // n = 3 * x2 - y2; n -= 2 * y2; // Оптимизация if ((i > j) && (n <= limit) && (n % 12 == 11)) is_prime[n] = !is_prime[n]; } } // Отсеиваем кратные квадратам простых чисел в интервале [5, sqrt(limit)]. // (основной этап не может их отсеять) for (i = 5; i <= sqr_lim; i++) { if (is_prime[i]) { n = i * i; for (j = n; j <= limit; j += n) { is_prime[j] = false; } } } // Вывод списка простых чисел в консоль. printf("2, 3, 5"); for (i = 6; i <= limit; i++) { // добавлена проверка делимости на 3 и 5. В оригинальной версии алгоритма потребности в ней нет. if ((is_prime[i]) && (i % 3 != 0) && (i % 5 != 0)){ printf(", %d", i); } }
Объяснение
- Все числа, равные (по модулю 60) 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56 или 58, делятся на два и заведомо не простые. Все числа, равные (по модулю 60) 3, 9, 15, 21, 27, 33, 39, 45, 51 или 57, делятся на три и тоже не являются простыми. Все числа, равные (по модулю 60) 5, 25, 35 или 55, делятся на пять и также не простые. Все эти остатки (по модулю 60) игнорируются.
- Все числа, равные (по модулю 60) 1, 13, 17, 29, 37, 41, 49 или 53, имеют остаток от деления на 4, равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 4x² + y² = n нечётно и само число не кратно никакому квадрату простого числа (en:square-free integer).
- Числа, равные (по модулю 60) 7, 19, 31, или 43, имеют остаток от деления на 6, равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² + y² = n нечётно и само число не кратно никакому квадрату простого.
- Числа, равные (по модулю 60) 11, 23, 47, или 59, имеют остаток от деления на 12, равный 11. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² − y² = n нечётно и само число не кратно никакому квадрату простого.
Ни одно из рассматриваемых чисел не делится на 2, 3, или 5, соответственно, они не могут делиться и на их квадраты. Поэтому проверка, что число не кратно квадрату простого числа, не включает 2², 3², и 5².
Особенности полной версии алгоритма
Сегментация
Для уменьшения требований к памяти «просеивание» производится порциями (сегментами, блоками), размер которых составляет примерно
 .
.Предпросеивание
Для ускорения работы полная версия алгоритма игнорирует все числа, которые кратны одному из нескольких первых простых чисел (2, 3, 5, 7, …). Это делается путем использования стандартных структур данных и алгоритмов их обработки[3], предложенных ранее Полом Притчардом (англ. Pritchard, Paul). Они известны под названием англ. wheel sieving. Количество первых простых чисел выбирается в зависимости от заданного числа N. Теоретически предлагается брать первые простые примерно до
 . Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель
. Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель  . При этом требуется дополнительная память, которая с ростом N ограничена как
. При этом требуется дополнительная память, которая с ростом N ограничена как  . Увеличение требований к памяти оценивается как
. Увеличение требований к памяти оценивается как  .
.Версия, представленная на сайте авторов, оптимизирована для поиска всех простых чисел до миллиарда (
 ), в ней исключаются из вычислений числа кратные двум, трём, пяти и семи (2 × 3 × 5 × 7 = 210).
), в ней исключаются из вычислений числа кратные двум, трём, пяти и семи (2 × 3 × 5 × 7 = 210).Оценка сложности
По оценке авторов алгоритм имеет асимптотическую сложность
 и требует
и требует  бит памяти. Ранее были известны алгоритмы столь же асимптотически быстрые, но требующие существенно больше памяти[4][5]: Теоретически в данном алгоритме сочетается максимальная скорость работы при меньших требованиях к памяти. Реализация алгоритма, выполненная одним из авторов, показывает достаточно высокую практическую скорость.
бит памяти. Ранее были известны алгоритмы столь же асимптотически быстрые, но требующие существенно больше памяти[4][5]: Теоретически в данном алгоритме сочетается максимальная скорость работы при меньших требованиях к памяти. Реализация алгоритма, выполненная одним из авторов, показывает достаточно высокую практическую скорость.См. также
Ссылки
- ↑ (англ.) A.O.L. Atkin, D.J. Bernstein, Prime sieves using binary quadratic forms, (в свободном доступе) (1999).
A.O.L. Atkin, D.J. Bernstein, Prime sieves using binary quadratic forms, Math. Comp. 73 (2004), 1023—1030. [более новая версия] - ↑ Оригинальный исходный текст доступен на сайте автора
- ↑ Pritchard, Paul Explaining the wheel sieve. (англ.) // Acta Informatica. — 1982. — Т. 17. — С. 477—485.
- ↑ Pritchard, Paul A sublinear additive sieve for finding prime numbers. (англ.) // Comm. ACM. — 1981. — Т. 24. — № 1. — С. 18—23.
- ↑ Brain Dunten, Julie Jones, Jonathan Sorenson A Space-Efficient Fast Prime Numbers Sieve (англ.) // Infomation Processing Letters. — 1996. — № 59. — С. 79—84.
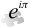 Категория:
Категория:- Теоретико-числовые алгоритмы
Wikimedia Foundation. 2010.
