- Код Хэмминга
-
Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей.В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 9 июля 2011.Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Содержание
История
В середине 1940-х годов Ричард Хэмминг работал в знаменитых Bell Labs на счётной машине Bell Model V. Это была электромеханическая машина, использующая релейные блоки, скорость которых была очень низка: один оборот за несколько секунд. Данные вводились в машину с помощью перфокарт, и поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.
Хэмминг часто работал в выходные дни, и все больше и больше раздражался, потому что часто был должен перезагружать свою программу из-за ненадежности перфокарт. На протяжении нескольких лет он проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 году он опубликовал способ, который на сегодняшний день известен как код Хэмминга.
Систематические коды
Систематические коды образуют большую группу из блочных, разделимых кодов (в которых все символы можно разделить на проверочные и информационные). Особенностью систематических кодов является то, что проверочные символы образуются в результате линейных операций над информационными символами. Кроме того, любая разрешенная кодовая комбинация может быть получена в результате линейных операций над набором линейно независимых кодовых комбинаций.
Самоконтролирующиеся коды
Коды Хэмминга являются самоконтролирующимися кодами, то есть кодами, позволяющими автоматически обнаруживать ошибки при передаче данных. Для их построения достаточно приписать к каждому слову один добавочный (контрольный) двоичный разряд и выбрать цифру этого разряда так, чтобы общее количество единиц в изображении любого числа было, например, четным. Одиночная ошибка в каком-либо разряде передаваемого слова (в том числе, может быть, и в контрольном разряде) изменит четность общего количества единиц. Счетчики по модулю 2, подсчитывающие количество единиц, которые содержатся среди двоичных цифр числа, могут давать сигнал о наличии ошибок.
При этом невозможно узнать, в каком именно разряде произошла ошибка, и, следовательно, нет возможности исправить её. Остаются незамеченными также ошибки, возникающие одновременно в двух, в четырёх или вообще в четном количестве разрядов. Впрочем, двойные, а тем более четырёхкратные ошибки полагаются маловероятными.
Самокорректирующиеся коды
Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для построения самокорректирующегося кода, рассчитанного на исправление одиночных ошибок, одного контрольного разряда недостаточно. Как видно из дальнейшего, количество контрольных разрядов k должно быть выбрано так, чтобы удовлетворялось неравенство
 или
или  , где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.
, где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.Диапазон m kmin 1 2 2-4 3 5-11 4 12-26 5 27-57 6 В настоящее время наибольший интерес представляют двоичные блочные корректирующие коды. При использовании таких кодов информация передаётся в виде блоков одинаковой длины и каждый блок кодируется и декодируется независимо друг от друга. Почти во всех блочных кодах символы можно разделить на информационные и проверочные. Таким образом, все комбинации кодов разделяются на разрешенные (для которых соотношение информационных и проверочных символов возможно) и запрещенные.
Основными характеристиками самокорректирующихся кодов являются:
- Число разрешенных и запрещенных комбинаций. Если n - число символов в блоке, r - число проверочных символов в блоке, k - число информационных символов, то
 - число возможных кодовых комбинаций,
- число возможных кодовых комбинаций,  - число разрешенных кодовых комбинаций,
- число разрешенных кодовых комбинаций,  - число запрещенных комбинаций.
- число запрещенных комбинаций. - Избыточность кода. Величину
 называют избыточностью корректирующего кода.
называют избыточностью корректирующего кода. - Минимальное кодовое расстояние. Минимальным кодовым расстоянием d называется минимальное число искаженных символов, необходимое для перехода одной разрешенной комбинации в другую.
- Число обнаруживаемых и исправляемых ошибок. Если g - количество ошибок, которое код способен исправить, то необходимо и достаточно, чтобы

- Корректирующие возможности кодов.
Граница Плоткина даёт верхнюю границу кодового расстояния
 или
или  при
при 
Граница Хемминга устанавливает максимально возможное число разрешенных кодовых комбинаций
 где
где  - число сочетаний из n элементов по i элементам. Отсюда можно получить выражение для оценки числа проверочных символов:
- число сочетаний из n элементов по i элементам. Отсюда можно получить выражение для оценки числа проверочных символов:  Для значений
Для значений  разница между границей Хемминга и границей Плоткина невелика.
разница между границей Хемминга и границей Плоткина невелика.Граница Варшамова-Гильберта для больших n определяет нижнюю границу числа проверочных символов
 Все вышеперечисленные оценки дают представление о верхней границе d при фиксированных n и k или оценку снизу числа проверочных символов
Все вышеперечисленные оценки дают представление о верхней границе d при фиксированных n и k или оценку снизу числа проверочных символовЛитература
- Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. М.: Мир, 1976, 600 c.
- Кларк Д., Кейн Д. Кодирование с исправлением ошибок в системах цифровой связи: Пер. с англ. М.: Радио и Связь,1987, 300 с.
Код Хемминга
Построение кодов Хемминга основано на принципе проверки на четность числа единичных символов: к последовательности добавляется элемент такой, чтобы число единичных символов в получившейся последовательности было четным.
 знак
знак  здесь означает сложение по модулю 2
здесь означает сложение по модулю 2 .
.  - ошибки нет,
- ошибки нет,  однократная ошибка. Такой код называется
однократная ошибка. Такой код называется  или
или  . Первое число - количество элементов последовательности, второе - количество информационных символов. Для каждого числа проверочных символов
. Первое число - количество элементов последовательности, второе - количество информационных символов. Для каждого числа проверочных символов  существует классический код Хемминга с маркировкой
существует классический код Хемминга с маркировкой  т.е. -
т.е. -  . При иных значениях k получается так называемый усеченных код, например международный телеграфный код МТК-2, у которого
. При иных значениях k получается так называемый усеченных код, например международный телеграфный код МТК-2, у которого  . Для него необходим код Хемминга
. Для него необходим код Хемминга  , который является усеченным от классического
, который является усеченным от классического  . Для Примера рассмотрим классический код Хемминга
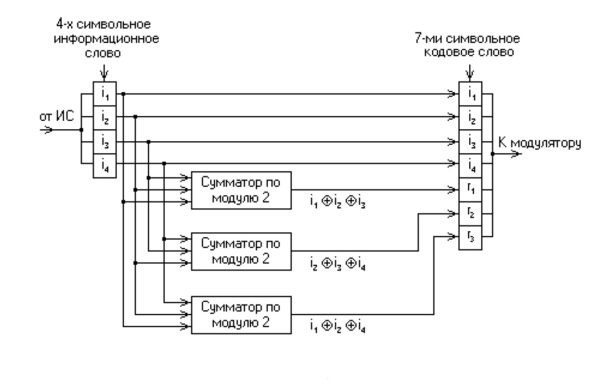
. Для Примера рассмотрим классический код Хемминга  . Сгруппируем проверочные символы следующим образом:
. Сгруппируем проверочные символы следующим образом:знак
 здесь означает сложение по модулю 2.
здесь означает сложение по модулю 2.- Получение кодового слова выглядит следующим образом:

 =
= 
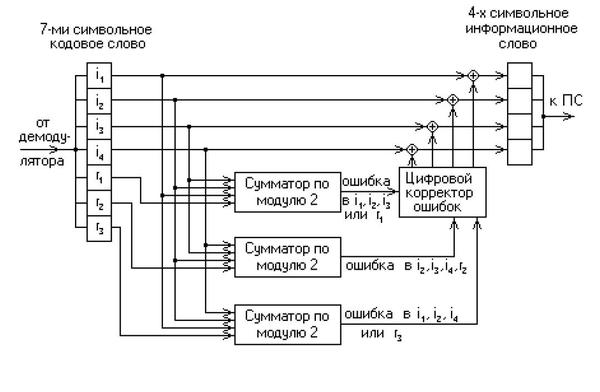
На вход декодера поступает кодовое слово
 где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:
где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов: называется синдромом последовательности.
называется синдромом последовательности.- Получение синдрома выглядит следующим образом:

 =
= 
Кодовые слова
 кода Хемминга
кода Хемминга






0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 1 0 1 0 0 1 1 1 0 1 0 1 1 0 0 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 1 0 1 0 1 0 0 1 1 1 0 1 1 0 0 0 1 1 0 0 0 1 0 1 1 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 Синдром
 указывает на то, что в последовательности нет искажений. Каждому ненулевому синдрому соответствует определенная конфигурация ошибок, которая исправляется на этапе декодирования. Для кода
указывает на то, что в последовательности нет искажений. Каждому ненулевому синдрому соответствует определенная конфигурация ошибок, которая исправляется на этапе декодирования. Для кода  в таблице указаны ненулевые синдромы и соответствующие им конфигурации ошибок (для вида:
в таблице указаны ненулевые синдромы и соответствующие им конфигурации ошибок (для вида: 





 ).
).Синдром 001 010 011 100 101 110 111 Конфигурация ошибок 0000001 0000010 1000000 0000100 0100000 0010000 0001000 Ошибка в символе 






Литература
- Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. М.: Мир, 1976, 600 c.
- Пенин П.Е.,Филиппов Л.Н. Радиотехнические системы передачи информации. М.: Радио и Связь, 1984, 256 с.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер. с англ. М.: Мир, 1986, 576 с.
Применение
Код Хэмминга используется в некоторых прикладных программах в области хранения данных, особенно в RAID 2; кроме того, метод Хэмминга давно применяется в памяти типа ECC и позволяет «на лету» исправлять однократные и обнаруживать двукратные ошибки.
См. также
Категории:- Обнаружение и устранение ошибок
- Теория кодирования
- Число разрешенных и запрещенных комбинаций. Если n - число символов в блоке, r - число проверочных символов в блоке, k - число информационных символов, то
Wikimedia Foundation. 2010.