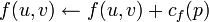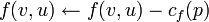- Алгоритм Форда — Фалкерсона
-
Алгоритм Форда — Фалкерсона
Алгоритм Форда — Фалкерсона решает задачу нахождения максимального потока в транспортной сети.
Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение 0: f(u,v) = 0 для всех
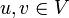 . Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.
. Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.Содержание
Алгоритм
Неформальное описание
- Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью.
- В остаточной сети находим любой путь из источника в сток. Если такого пути нет, останавливаемся.
- Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:
- На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью cmin.
- Для каждого ребра на найденном пути увеличиваем поток на cmin, а в противоположном ему - уменьшаем на cmin.
- Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.
- Возвращаемся на шаг 2.
Важно, что алгоритм не конкретизирует, какой именно путь мы ищем на шаге 2 или как мы это делаем. По этой причине алгоритм гарантированно сходится только для целых пропускных способностей, но даже для них при больших значениях пропускных способностей он может работать очень долго. Если пропускные способности вещественны, алгоритм может работать бесконечно долго, не сходясь к оптимальному решению (см. пример ниже).
Если искать не любой путь, а кратчайший, получится алгоритм Эдмондса-Карпа или алгоритм Диница. Эти алгоритмы сходятся для любых вещественных весов за время O( | V | | E | 2) и O( | V | 2 | E | ) соответственно.
Формальное описание
Дан граф G(V,E) с пропускной способностью c(u,v) и потоком f(u,v) = 0 для ребер из u в v. Необходимо найти максимальный поток из источника s в сток t. На каждом шаге алгоритма действуют те же условия, что и для всех потоков:
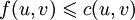 . Поток из u в v не превосходит пропускной способности.
. Поток из u в v не превосходит пропускной способности.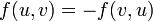 .
.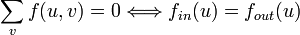 для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.
для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.
Остаточная сеть Gf(V,Ef) — сеть с пропускной способностью cf(u,v) = c(u,v) − f(u,v) и без потока.
Вход Граф
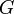 с пропускной способностью
с пропускной способностью  , источник
, источник  и сток
и сток 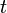
Выход Максимальный поток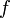 из
из  в
в 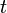
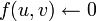 для всех ребер
для всех ребер 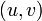
- Пока есть путь
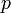 из
из  в
в 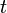 в
в 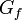 , такой что
, такой что 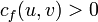 для всех ребер
для всех ребер 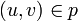 :
:
- Найти
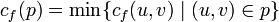
- Для каждого ребра
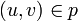
- Найти
Путь может быть найден, например, поиском в ширину (алгоритм Эдмондса-Карпа) или поиском в глубину в Gf(V,Ef).
Сложность
Добавляя поток увеличивающего пути к уже имеющемуся потоку, максимальный поток будет получен, когда нельзя будет найти увеличивающий путь. Тем не менее, если величина пропускной способности — иррациональное число, то алгоритм может работать бесконечно. В целых числах таких проблем не возникает и время работы ограничено O(E*f), где E — число рёбер в графе, f — максимальный поток в графе, так как каждый увеличивающий путь может быть найден за O(E) и увеличивает поток как минимум на 1.
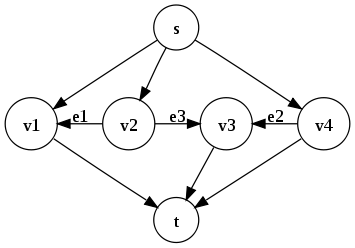
Пример не сходящегося алгоритма
Рассмотрим приведённую справа сеть, с источником
 , стоком
, стоком 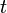 , пропускными способностями рёбер
, пропускными способностями рёбер 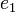 ,
, 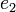 и
и 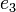 соответственно
соответственно 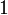 ,
, 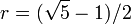 и
и 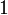 и пропускной способностью всех остальных рёбер, равной целому числу
и пропускной способностью всех остальных рёбер, равной целому числу 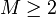 . Константа
. Константа 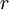 выбрана так, что
выбрана так, что 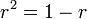 . Мы используем пути из остаточного графа, приведённые в таблице, причём
. Мы используем пути из остаточного графа, приведённые в таблице, причём 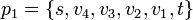 ,
, 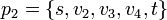 и
и 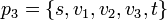 .
.Шаг Найденный путь Добавленный поток Остаточные пропускные способности e1 e2 e3 0 r0 = 1 r 1 1 {s,v2,v3,t} 1 r0 r1 0 2 p1 r1 r2 0 r1 3 p2 r1 r2 r1 0 4 p1 r2 0 r3 r2 5 p3 r2 r2 r3 0 Заметим, что после шага 1, как и после шага 5, остаточные способности рёбер e1, e2 и e3 имеют форму rn, rn + 1 and 0, соответственно, для какого-то натурального n. Это значит, что мы можем использовать увеличивающие пути p1, p2, p1 и p3 бесконечно много раз, и остаточные пропускные способности этих рёбер всегда будут в той же форме.Полный поток после шага 5 равен 1 + 2(r1 + r2). За бесконечное время полный поток сойдётся к
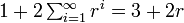 , тогда как максимальный поток равен 2M + 1. Таким образом, алгоритм не только работает бесконечно долго, но даже и не сходится к оптимальному решению.[1]
, тогда как максимальный поток равен 2M + 1. Таким образом, алгоритм не только работает бесконечно долго, но даже и не сходится к оптимальному решению.[1]Пример
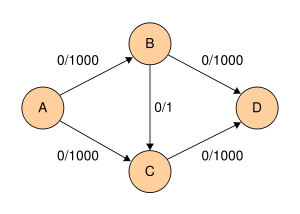
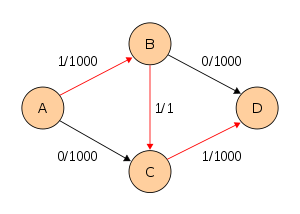
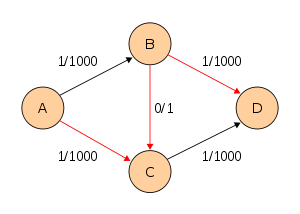
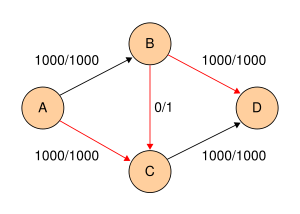
Следующий пример показывает первые шаги алгоритма Форда-Фалкерсона в транспортной сети с четырьмя узлами, источником A и стоком D. Этот пример показывает худший случай. При использовании поиска в ширину алгоритму потребуется всего лишь 2 шага.
См. также
Cсылки
- Анимация
- Визуализатор алгоритма
- Реализация поиска максимальнго потока методом Форда-Фалкерсона на Java
Литература
- Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
Сноски
- ↑ Zwick, Uri (21 August 1995). «The smallest networks on which the Ford-Fulkerson maximum flow procedure may fail to terminate». Theoretical Computer Science 148 (1): 165–170. DOI:10.1016/0304-3975(95)00022-O.
Wikimedia Foundation. 2010.