Квадрирование квадрата

Разбиение квадрата на 21 квадрат, среди которых нет равных. Цифра внутри каждого квадрата означает длину его стороны. Соответственно, длина стороны большого квадрата равна (складывая длины сторон крайних квадратов) 50 + 35 + 27 = 50 + 29 + 33 = 33 + 37 + 42 = 27 + 19 + 24 + 42 = 112

Квадри́рование квадра́та — задача о разбиении квадрата на конечное число меньших квадратов. В более узком смысле — задача о разбиении квадрата на конечное число попарно неравных между собой квадратов.

Долгое время считалось, что эта чрезвычайно трудная математическая задача неразрешима. В 1936—1938 годах её решили четыре студента Тринити-колледжа Кембриджского университета ^[1].

Диаграмма Смита

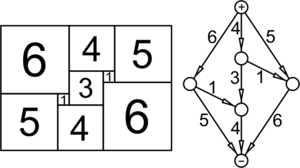Диаграмма Смита для прямоугольника. Верхняя клемма «+» соответствует верхней стороне прямоугольника, нижняя клемма «−» — нижней стороне. Остальные клеммы соответствуют промежуточным горизонтальным отрезкам. Если длине стороны квадрата сопоставить силу тока, то диаграмма становится электрической схемой, для которой выполняется закон Кирхгофа. Например, длина верхней стороны прямоугольника складывается из сторон 6 + 4 + 5 = 15, что соответствует разветвлению тока в 15 единиц на три соответствующие части

Ключевую роль в решении задачи квадрирования сыграло изобретение диаграммы, названной диаграммой Смита, которая любому разбиению квадрата (или прямоугольника) ставит в соответствие эквивалентную электрическую цепь. Каждому горизонтальному отрезку на схеме разбиения квадрата соответствует «клемма» этой цепи, а каждому квадрату разбиения — проводник, соединяющий две «клеммы». Сила тока, текущего по проводнику, равна длине стороны соответствующего квадрата. Если считать сопротивление каждого проводника равным единице, такая электрическая цепь ведёт себя как «настоящая» и подчиняется правилам Кирхгофа для токов в цепи. Это позволило применять для решения задачи квадрирования хорошо разработанную теорию электрических цепей.

Терминология

Квадрат, разбитый на попарно неравные квадраты, называется совершенным.

Порядком квадрата, разбитого на составные квадраты, называется число составляющих его квадратов.

Разбиение квадрата, никакое подмножество квадратов которого не образует прямоугольника (не считая отдельных квадратов), называется простым.

Краткая история

Самые первые найденные Бруксом, Смитом, Стоуном и Таттом совершенные квадраты были 69-го порядка. В 1939 году Р. Шпраг (R. Sprague) нашёл совершенный квадрат 55-го порядка, это был первый опубликованный совершенный квадрат. Позднее Т. Г. Уиллкокс (T. H. Willcocks) нашёл совершенный квадрат 24-го порядка, который долгое время держал рекорд малости порядка.

Наконец, в 1978 году голландский математик А. Й. В. Дуйвестэйн (A. J. W. Duijvestijn) с помощью компьютера нашёл разбиение квадрата на 21 квадрат, среди которых нет равных. Он доказал, что не существует совершенного квадрата меньшего порядка, а также показал, что найденное им разбиение — единственно возможное для 21-го порядка.

Кубирование куба

«Кубирование куба», то есть разбиение куба на конечное число попарно неравных между собой кубов невозможно. Доказательство этого факта было дано Бруксом, Смитом, Стоуном и Таттом.

Идея доказательства состоит в следующем. Допустим, что искомое разбиение куба существует. Среди всех кубов разбиения, стоящих на нижнем основании исходного куба, выберем наименьший. Назовём его кубом A. Поскольку к A прилегают с боков только бо́льшие кубы разбиения, их грани будут возвышаться над ним со всех сторон, образуя «стены». Отсюда ясно, что на верхнем основании A могут стоять только кубы меньших размеров.

Выберем среди них наименьший и обозначим его B. При этом, B не может стоять на краю куба A, так как при квадрировании квадрата наименьший квадрат не может быть с краю.

Повторяя для него те же рассуждения, что и для A, приходим к выводу о существовании ещё меньшего куба C, стоящего на верхнем основании B. Повторяя эти рассуждения, мы получаем бесконечную последовательность кубов разбиения, что противоречит нашему предположению о конечности разбиения.

Аналогично, невозможно «гиперкубирование гиперкуба» для гиперкубов любой размерности, большей 3-х. Действительно, для любой размерности n гиперкубы разбиения, прилегающие к какой-либо (n − 1)-мерной гиперграни исходного гиперкуба, должны разбивать эту гипергрань на конечное число попарно неравных (n − 1)-мерных гиперкубов. При n = 4 «гиперкубирование» невозможно, так как должно порождать «кубирование» 3-мерных гиперграней исходного 4-мерного гиперкуба. Индукцией по n можно сделать заключение о невозможности «гиперкубирования» для всех n > 3.

Литература

• М. Гарднер, Математические головоломки и развлечения. Пер. с английского Ю. Данилова. Изд. «Оникс», Москва, 1994, стр. 305—326.
• И. М. Яглом, Как разрезать квадрат серия «Математическая библиотечка» М., Наука, 1968—112 с.
• C. J. Bouwkamp and A. J. W. Duijvestijn, Catalogue of Simple Perfect Squared Squares of Orders 21 Through 25, Eindhoven Univ. Technology, Dept. of Math., Report 92-WSK-03, Nov. 1992.
• C. J. Bouwkamp and A. J. W. Duijvestijn, Album of Simple Perfect Squared Squares of order 26, Eindhoven University of Technology, Faculty of Mathematics and Computing Science, EUT Report 94-WSK-02, December 1994.
• Brooks, R. L.; Smith, C. A. B.; Stone, A. H.; and Tutte, W. T. The Dissection of Rectangles into Squares, Duke Math. J. 7, 312—340, 1940
• Martin Gardner, Squaring the square, in The 2nd Scientific American Book of Mathematical Puzzles and Diversions.
• H. Meschkowski, Unsolved and Unsolvable Problems in Geometry, Oliver and Boyd, 1966, Edinburgh, pp. 9—102.
• S. Stein, Mathematics: The Man-Made Universe, (2nd ed.) Freeman and Co., 1969, San Francisco, pp. 92—124.
• W. Tutte, Squaring the Square, Canadian journal of Mathematics, 1950, pp.197—209.
• W. Tutte, The Quest of the Perfect Square, The American Mathematical Monthly, 1965, Vol. 72, No. 2, pp. 29—35.

1. ↑ Brooks, R. L.; Smith, C. A. B.; Stone, A. H.; and Tutte, W. T. The Dissection of Rectangles into Squares, Duke Math. J. 7, 312—340, 1940

Ссылки

• http://www.math.uwaterloo.ca/navigation/ideas/articles/honsberger2/index.shtml
• http://www.math.niu.edu/~rusin/known-math/98/square_dissect
• http://www.stat.ualberta.ca/people/schmu/preprints/sq.pdf
• http://karl.kiwi.gen.nz/prosqtre.html
• http://karl.kiwi.gen.nz/prosqtsq.html