- Компьютер для операций с функциями
-
Компьютер для операций с математическими функциями (в отличие от обычного компьютера) оперирует с функциями на аппаратном уровне (то есть без программирования этих операций).[1][2][3]
Содержание
История
Вычислительная машина для операций с функциями была предложена и разработана Карцевым в 1967 году[1]. В число операций этой вычислительной машины входили сложение, вычитание и умножение функций, сравнение функций, аналогичные операции над функцией и числом, отыскание максимума функций, вычисление неопределенного интеграла, вычисление определенного интеграла от производной двух функций, сдвиг функции по абсциссе и т. д. По архитектуре эта вычислительная машина являлась (пользуясь современной терминологией) векторным процессором. В ней использовался тот факт, что многие из этих операций могут быть истолкованы как известные операции над векторами: сложение и вычитание функций — как сложение и вычитание векторов, вычисление определенного интеграла от производной двух функций — как вычисление скалярного произведения двух векторов, сдвиг функций по абсциссе — как поворот вектора относительно осей координат и т. д.[1] В 1966 году Хмельник предложил метод кодирования функций[2] , то есть представления функции единым (для функции в целом) позиционным кодом. При этом указанные операции с функциями выполняются как уникальные машинные операции с такими кодами на единственном арифметическом устройстве[3]
Позиционные коды функций одного аргумента[2][3]
См. также: Позиционное кодирование (значения)Основная идея
Позиционный код целого числа
 представляет собой запись цифр
представляет собой запись цифр  этого числа в некоторой позиционной системе счисления, имеющую вид
этого числа в некоторой позиционной системе счисления, имеющую видТакой код можно назвать линейным. В отличие от него позиционный код функции
 одного аргумента
одного аргумента  имеет вид
имеет видто есть является плоским и треугольным, поскольку цифры в нем образуют треугольник.
Указанному позиционному коду целого числа соответствует сумма вида ,.
,.
где
 — основание данной системы счисления. Указанному позиционному коду функции одного аргумента соответствует двойная сумма вида
— основание данной системы счисления. Указанному позиционному коду функции одного аргумента соответствует двойная сумма вида ,
,
где
 — целое положительное число, количество значений цифры
— целое положительное число, количество значений цифры  ,
,  — определенная функция аргумента
— определенная функция аргумента  .
.
Сложение позиционных кодов чисел связано с передачей переноса в старший разряд по схеме .
.
Сложение позиционных кодов функций одного аргумента также связано с передачей переноса по схеме
 .
.
При этом один и тот же перенос передается одновременно в два старших разряда.
R-е треугольные коды
Треугольный код называется R-м (и обозначается как
 ), если числа
), если числа  принимают значения из множества
принимают значения из множества где
где  и
и  .
.
Например, треугольный код является троичным
 , если
, если  , и — четверичным
, и — четверичным  , если
, если  .
.
Для R-х треугольных кодов справедливы следующие равенства: ,
,
где a — любое число. Существует
 любого целого действительного числа. В частности,
любого целого действительного числа. В частности,  . Также существует
. Также существует  любой функции вида
любой функции вида  . В частности,
. В частности,  .
.Одноразрядное сложение
в R-х треугольных кодах состоит в том, что
- в данном
 -разряде определяется сумма
-разряде определяется сумма  слагаемых разрядов
слагаемых разрядов  и двух переносов
и двух переносов  , поступивших в данный разряд слева, то есть
, поступивших в данный разряд слева, то есть
 ,
,
- эта сумма представляется в виде
 , где
, где  ,
,  записывается в
записывается в  -разряд суммарного кода, а перенос
-разряд суммарного кода, а перенос  из данного разряда передается в
из данного разряда передается в  -разряд и
-разряд и  -разряд.
-разряд.
Эта процедура описывается (как и при одноразрядном сложении чисел) таблицей одноразрядного сложения, где должны присутствовать все значения слагаемых
 и
и  и все значения переносов, возникающих при разложении суммы
и все значения переносов, возникающих при разложении суммы  . Такая таблица может быть синтезирована при
. Такая таблица может быть синтезирована при 
Ниже приведена таблица одноразрядного сложения при :
:Smk TK(Smk) 

. . 0 . . 0 0 0 0 0 . . 0 . . 1 1 0 1 0 . . 0 . . (-1) (-1) 0 (-1) 0 . . 1 . . 2 (-1) 1 (-1) 1 . . 1 . . 3 0 1 0 1 . . 1 . . 4 1 1 1 1 . . (-1) . . (-2) 1 (-1) 1 (-1) . . (-1) . . (-3) 0 (-1) 0 (-1) . . (-1) . . (-4) (-1) (-1) (-1) (-1) Одноразрядное вычитание
в R-х треугольных кодах отличается от одноразрядного сложения только тем, что в данном
 -разряде величина
-разряде величина  определяется по формуле
определяется по формуле .
.
Одноразрядное деление на параметр R
в R-х треугольных кодах основано на использовании соотношения
 ,
,
откуда следует, что деление каждого разряда вызывает переносы в два нижних разряда. Следовательно, разрядный результат в этой операции является суммой частного от деления данного разряда на R и переносов из двух верхних разрядов. Таким образом, при делении на параметр R
- в данном
 -разряде определяется сумма
-разряде определяется сумма
 ,
,
- эта сумма представляется в виде
 , где
, где  ,
,  записывается в
записывается в  -разряд результирующего кода, а перенос
-разряд результирующего кода, а перенос  из данного разряда передается в
из данного разряда передается в  -разряд и
-разряд и  -разряд.
-разряд.
Эта процедура описывается таблицей одноразрядного деления на параметр R, где должны присутствовать все значения слагаемых и все значения переносов, возникающих при разложении суммы
 . Такая таблица может быть синтезирована при
. Такая таблица может быть синтезирована при 
Ниже приведена таблица одноразрядного деления на параметр R при :
:Smk TK(Smk) 

. . 0 . . 0 0 0 0 0 . . 1 . . 1 0 0 1 0 . . (-1) . . (-1) 0 0 (-1) 0 . . 0 . . 1/3 1 (-1/3) 0 1 . . 1 . . 2/3 (-1) 1/3 1 (-1) . . 1 . . 4/3 1 (-1/3) 1 1 . . 2 . . 5/3 (-1) 1/3 2 (-1) . . 0 . . (-1/3) (-1) 1/3 0 (-1) . . (-1) . . (-2/3) 1 (-1/3) (-1) 1 . . (-1) . . (-4/3) (-1) 1/3 (-1) (-1) . . (-2) . . (-5/3) 1 (-1/3) (-2) 1 Сложение и вычитание
R-х треугольных кодов состоит (как и в позиционных кодах чисел) в последовательно выполняемых одноразрядных операциях. При этом одноразрядные операции во всех разрядах каждого столбца выполняются одновременно.
Умножение
R-х треугольных кодов. Умножение некоторого кода
 на
на  -разряд другого кода
-разряд другого кода  заключается в
заключается в  -сдвиге кода
-сдвиге кода  , то есть сдвиге его на k столбцов влево и на m строк вверх. Умножение кодов
, то есть сдвиге его на k столбцов влево и на m строк вверх. Умножение кодов  и
и  заключается в последовательных
заключается в последовательных  -сдвигах кода
-сдвигах кода  и сложениях сдвинутого кода
и сложениях сдвинутого кода  с частичным произведением (как и в позиционных кодах чисел).
с частичным произведением (как и в позиционных кодах чисел).Дифференцирование
R-х треугольных кодов. Производная функции
 , определенной выше,
, определенной выше, .
.
Поэтому дифференцирование треугольных кодов функции
 заключается в определении треугольного кода частной производной
заключается в определении треугольного кода частной производной  и умножении его на известный треугольный код производной
и умножении его на известный треугольный код производной  . Определение треугольного кода частной производной
. Определение треугольного кода частной производной  основано на соотношении
основано на соотношении .
.
Cпособ дифференцирования заключается в организации переносов из mk-разряда в (m+1,k)-разряд и в (m-1,k)-разряд, а их суммирование в данном разряде производится аналогично одноразрядному сложению.
Кодирование и декодирование
R-х треугольных кодов. Функция, представленная рядом вида
 ,
,
с целыми коэффициентами
 , может быть представлена R-м треугольным кодом, так как эти коэффициенты и функции
, может быть представлена R-м треугольным кодом, так как эти коэффициенты и функции  имеют R-е треугольные коды (о чем сказано в начале раздела). С другой стороны, R-й треугольный код может быть представлен указанным рядом, так как любое слагаемое
имеют R-е треугольные коды (о чем сказано в начале раздела). С другой стороны, R-й треугольный код может быть представлен указанным рядом, так как любое слагаемое  в позиционном разложении функции (соответствующем этому коду) может быть представлено таким же рядом.
в позиционном разложении функции (соответствующем этому коду) может быть представлено таким же рядом.Укорочение
R-х треугольных кодов. Так называется операция уменьшения числа ненулевых столбцов. Необходимость укорочения возникает при возникновении переносов за разрядную сетку. Укорочение заключается в делении на параметр R. При этом все коэффициенты представимого кодом ряда уменьшаются в R раз, а дробные части этих коэффициентов отбрасываются. Исчезает также старший член ряда. Такое сокращение допустимо, если известно, что ряды функций являются сходящимися. Укорочение состоит в последовательно выполняемых одноразрядных операциях деления на параметр R. При этом одноразрядные операции во всех разрядах каждой строки выполняются одновременно, а переносы из младшей строки отбрасываются.
Масштабный коэффициент
R-й треугольный код сопровождается масштабным коэффициентом M, аналогичным порядку в числе с плавающей точкой. Коэффициент M позволяет представить все коэффиценты кодируемого ряда в виде целых чисел. Коэффициент M умножается на R при укорочении кода. При сложении коэффициенты M выравниваются, для чего необходимо укорачивать один из слагаемых кодов. При умножении коэффициенты M также умножаются.
Позиционные коды функций многих аргументов[4]
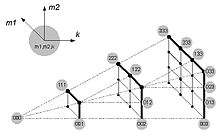
Позиционный код функции двух аргументов изображен на рис. 1. Ему соответствует тройная сумма вида
 ,
,
где
 — целое положительное число, количество значений цифры
— целое положительное число, количество значений цифры  , а
, а  — определенные функции аргументов
— определенные функции аргументов  соответственно. На рис. 1 узлы соответствуют цифрам
соответственно. На рис. 1 узлы соответствуют цифрам  , а в кружках показаны значения индексов
, а в кружках показаны значения индексов  соответствующей цифры. Позиционный код функции двух аргументов называется пирамидальным. Позиционный код называется R-м (и обозначается как
соответствующей цифры. Позиционный код функции двух аргументов называется пирамидальным. Позиционный код называется R-м (и обозначается как  ), если числа
), если числа  принимают значения из множества
принимают значения из множества  . При сложении кодов
. При сложении кодов  перенос распространяется в четыре разряда и поэтому
перенос распространяется в четыре разряда и поэтому  .
.Позиционному коду функции нескольких аргументов соответствует сумма вида
 ,
,
где
 — целое положительное число, количество значений цифры
— целое положительное число, количество значений цифры  , а
, а  — определенные функции аргументов
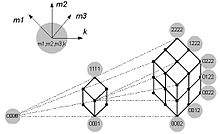
— определенные функции аргументов  . Позиционный код функции нескольких аргументов называется гиперпирамидальным. На рис. 2 показан для примера позиционный гиперпирамидальный код функции трех аргументов. В нем узлы соответствуют цифрам
. Позиционный код функции нескольких аргументов называется гиперпирамидальным. На рис. 2 показан для примера позиционный гиперпирамидальный код функции трех аргументов. В нем узлы соответствуют цифрам  , а в кружках показаны значения индексов
, а в кружках показаны значения индексов  соответствующей цифры. Позиционный гиперпирамидальный код называется R-м (и обозначается как
соответствующей цифры. Позиционный гиперпирамидальный код называется R-м (и обозначается как  ), если числа
), если числа  принимают значения из множества
принимают значения из множества  . При сложении кодов
. При сложении кодов  перенос распространяется в a-мерный куб, содержащий
перенос распространяется в a-мерный куб, содержащий  разрядов и поэтому
разрядов и поэтому  .
.Примечания
- ↑ 1 2 3 Малиновский Б. Н. История вычислительной техники в лицах. — Киев, Фирма "КИТ", ПТОО "АСК". — 1995. — ISBN 5-7707-6131-8
- ↑ 1 2 3 Хмельник С. И. Кодирование функций // Кибернетика, АН УССР. — 1966. — Т. 4.
- ↑ 1 2 3 Хмельник С. И. Компьютерная арифметика функций. Алгоритмы и аппаратура. — Mathematics in Computers. — Россия-Израиль, 2004. — ISBN 978-0-557-07520-1
- ↑ Хмельник С. И. Несколько типов позиционных кодов функций // Кибернетика, АН УССР. — 1970. — Т. 5.
Технологии цифровых процессоров Архитектура CISC · EDGE · EPIC · MISC · URISC · RISC · VLIW · ZISC · Фон Неймана · Гарвардская
8 бит · 16 бит · 32 бит · 64 бит · 128 битПараллелизм Pipeline Конвейер · In-Order & Out-of-Order execution · Переименование регистров · Speculative execution Уровни Бит · Инструкций · Суперскалярность · Данных · Задач Потоки Многопоточность · Simultaneous multithreading · Hyperthreading · Superthreading · Аппаратная виртуализация Классификация Флинна SISD · SIMD · MISD · MIMD Реализации DSP · GPU · SoC · PPU · Векторный процессор · Математический сопроцессор • Микропроцессор · Микроконтроллер Компоненты Barrel shifter · FPU · BSB · MMU · TLB · Регистровый файл · control unit · АЛУ • Демультиплексор · Мультиплексор · Микрокод · Тактовая частота • Корпус • Регистры • Кэш (Кэш процессора) Управление питанием APM · ACPI · Clock gating · Динамическое изменение частоты • Динамическое изменение напряжения Категории:- Технологии процессоров
- Классы компьютеров
- Вычислительная техника
- Функции
Wikimedia Foundation. 2010.