- Rabbit
-
Rabbit - высокоскоростной поточный шифр впервые представленный [1] в феврале 2003 года на 10-м симпозиуме FSE. В мае 2005, он был отправлен на конкурс eStream, целью которого было создание европейских стандартов для поточных систем шифрования.
Разработчиками Rabbit являются Martin Boesgaard, Mette Vesterager, Thomas Pedersen, Jesper Christiansen и Ove Scavenius.
Rabbit используют 128-битный ключ и 64-битный инициализирующий вектор. Шифр был разработан с целью использования в программном обеспечении, как обладающий высокой скоростью шифрования. При этом скорость шифрования могла достигать 3.7 циклов в байт(CPB) для процессора Pentium 3 и 10.5 циклов в байт для ARM7. Тем не менее, шифр также оказался быстрым и компактным при реализации в аппаратном обеспчении.
Основным компонентом шифра является генератор битового потока, который шифрует 128 битов сообщения за итерацию. Достоинство шифра в тщательном перемешивании его внутренних состояний между двумя последовательными итерациями. Функция перемешивания полностью основана на арифметических операциях, доступных на современных процессорах, т.е. S-блоки подстановок и поисковые таблицы не нужны для реализации шифра.
Авторы шифра предоставили полный набор технических описаний на домашней странице Cryptico.[2]. Шифр также описан в RFC 4503. Cryptico обладала патентом на шифр, и многии годы для использования шифра в коммерческих целях требовалась лицензия. Однако, 6 октября 2008 шифр разрешили использовать для любых целях бесплатно. [3]
Содержание
Rabbit и eStream [4]
Конкурс eStream
Поточные симметричные шифры проекта eSTREAM составляют два профиля. В Профиль 1 входят шифры ориентированные на программную реализацию, а в Профиль 2 - шифры ориентированные на аппаратную реализацию.
Лучшие шифры проекта:
Профиль 1 Профиль 2 HC-128 F-FCSR-H v2 Rabbit Grain v1 Salsa20/12 MICKEY v2 Sosemanuk Trivium В Профиль 1 вошли поточные симметричные шифры с хорошей программной реализацией. На столько хорошей, что должны были превосходить по скоростным показателям блочный симметричный алгоритм шифрования AES в режимах генерации гаммы. Основным требованием к этому профилю было обеспечение уровня безопсности в 128 бит.
Достоинства и недостатки шифра Rabbit
Rabbit является одной из старейших конструкций проекта eSTREAM. Данный поточный шифр не был подвержен каким-либо модификациям или дополнениям. Его спецификация оставалась неизменной с 2003 года и по данный момент. Шифр пережил все три этапа проекта и не на одном не был подвержен криптоаналитическим атакам. Кроме всего прочего данный алгоритм очень хорошо реализуется на новых процессорах семейства Intel. Как недостаток можно заметить тот факт, что шифр Rabbit обеспечивает уровень безопасности только в 128 бит.
Результаты заключительного голосования проекта eSTREAM по Профилю 1.
Профиль 1 очки Rabbit 2.80 Salsa20 2.80 Sosemanuk 1.20 HC-128 0.60 NLS v2 -0.60 LEX v2 -1.20 CryptMT v3 -1.40 Dragon -1.60 Алгоритм
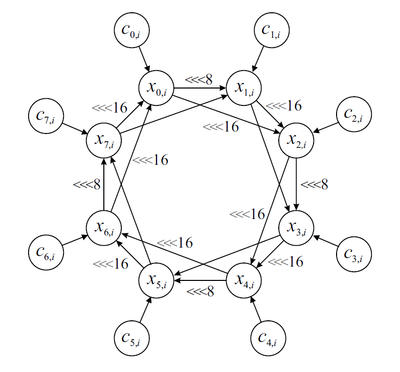
Внутреннее состояние поточного шифра содержит 513 битов. 512 из них поделены на 8-мь 32-битных переменных состояний
 и 8-мь 32-битных счетчиков
и 8-мь 32-битных счетчиков  , где
, где  - переменная состояния подсистемы
- переменная состояния подсистемы  при итерации
при итерации  , а
, а  - обозначает соответствующий счетчик переменных. 513-й бит - бит переноса φ
- обозначает соответствующий счетчик переменных. 513-й бит - бит переноса φ , который необходимо хранить между итерациями. Этот бит инициализируется нулем. 8-мь переменных состояний и 8-мь счетчиков зависят от ключа при инициализации.
, который необходимо хранить между итерациями. Этот бит инициализируется нулем. 8-мь переменных состояний и 8-мь счетчиков зависят от ключа при инициализации.Схема установки ключа
Алгоритм инициализируется расширением 128-битного ключа на 8 переменных состояния и 8 счетчиков так, что существует взаимнооднозначное соответствие между ключом, начальными переменными состояний,
 , и начальными счетчиками,
, и начальными счетчиками,  . Ключ,
. Ключ, ![K^{[127..0]}](4ea916b134ebe653e12c89d816d9acf8.png) , поделен на 8 подключей:
, поделен на 8 подключей: ![k_0^{[15..0]}](c9118db2c55c372c7e767d76d2e8a448.png) ,
, ![k_1^{[31..16]}](f4c7f0719f82b57efa9e67d0e178d7ff.png) , ... ,
, ... , ![k_7^{[127..112]}](24d9c2a91c446df39a2fd23e3fc3c5fb.png) , переменные состояний и счетчики инициализируются при помощи подключей:
, переменные состояний и счетчики инициализируются при помощи подключей:(где
 - операция конкатенации)
- операция конкатенации)Система прогоняется 4 раза, согласно функции следующего состояния, определенной ниже, чтобы понизить кореляцию между битами ключа и битами переменных внутренного состояния. В конце, счетчики ре-инициализируются следующим образом:
для предотвращения восстановления ключа путем инверсии системы счетчиков.
Функция следующего состояния
Здесь все сложения по модулю 2^32. Функции и
и  возвращают, соответственно, младшие и старшие четыре байта 64-разрядного числа
возвращают, соответственно, младшие и старшие четыре байта 64-разрядного числа  .
. - циклический сдвиг влево.
- циклический сдвиг влево.Система счетчиков
Уравнения, задающие изменение системы счетчиков:
где счетчик бита переноса, φ
 , задается:
, задается:
Кроме того, константы определяются как:
определяются как:Схема извлечения
После каждой итерации, 128 битов выхода генерируется по следующим формулам:
где
 128-ми битный блок шифрующего потока на
128-ми битный блок шифрующего потока на  -той итерации.
-той итерации.Схема шифрования и расшифрования
Выполняется операция XOR между извлеченными битами и текстом/шифротекстом для шифрования/дешифрования.
где
 и
и  обозначают
обозначают  -тый блок шифротекста и текста соответственно.
-тый блок шифротекста и текста соответственно.Свойства схемы установки ключа
Установку ключа можно разделить на три этапа: расширение ключа, система итераций, модификация счетчика.
- Этап расширения ключа гарантирует взаимно-однозначное соответствие между ключом состояния и ключом счетчика, который предотвращает избыток ключей. Он также распределяет биты ключа оптимальным образом для итераций.
- Система итераций гарантирует, что после одной итерации функции следующего состояния, каждый бит ключа повлияет на все восемь переменных состояния. Это также гарантирует, что после второй итерации функции следующего состояния все биты ключа повлияют на все биты состояния с вероятностью 0,5. Для надежности шифрования итерацию проделывают четыре раза.
- Даже если счетчики будут известны злоумышленнику, модификация счетчика сильно усложняет восстановление ключа путем инвертирования счетчика системы, так как потребуются сведения о переменных состояния, также это нарушает взаимно-однозначное соотношение между ключом и счетчиком.
Безопасность
Rabbit предоставляет 128-битную защиту против атакующих, чья цель один уникальный ключ. Если же атака происходит на несколько ключей за раз, и все равно, который из них взломают, то защищенность снижается до 96 бит.[5].
Атаки на функцию установления ключа
После того, как ключ задан, биты счетчика и состояния строго и очень нелинейно зависят от бит ключа. Это усложняет взлом для атак на основе угадывания части ключа. Даже если биты счетчика были известны после модификации счетчика. Конечно, знание счетчиков делает другие виды взломов легче.
Атака, основанная на коллизии
В шифре Rabbit используется неоднозначное отображение, разные ключи потенциально могут привести к той же гамме. Эта проблема в основном сводится к вопросу о том, что разные ключи приводят к одним и тем же значениям счетчика, так как различные значения счетчика почти наверняка приведут к разным генерациям гаммы. Надо обратить внимание, что расширение ключа и система итераций были разработаны таким образом, что каждый ключ приводит к уникальным значениям счетчика. Тем не менее, модификация счетчика может привести к равным значениям счетчика для двух различных ключей. Полагая, что после четырех начальных итераций, внутреннее состояние, по существу, случайное и не коррелирует с системой счетчиков, вероятность коллизий задается «парадоксом дней рождения», т.е. для всех
 ключей одна коллизия ожидается в 256-битным счетчиком. Таким образом, коллизия системы счетчиков не должна вызывать проблем на практике.
ключей одна коллизия ожидается в 256-битным счетчиком. Таким образом, коллизия системы счетчиков не должна вызывать проблем на практике.Атака со связанным ключом
Атака основана на использовании свойств симметрии в функциях следующего состояния и установки ключа. Рассмотрим, например, два ключа
 и
и  связанные соотношением
связанные соотношением ![K^{[i]} = \tilde K^{[i+2]}](27c79a671306512ddd0b191fee35c359.png) для всех
для всех  . Это приводит к соотношению
. Это приводит к соотношению  и
и  . Теперь рассмотрим, когда
. Теперь рассмотрим, когда  и
и  один и тот же ключ. Если условие
один и тот же ключ. Если условие  выполнено, то функция следующего состояния сохранила бы свойство симметрии. Но можно легко проверить, что константы
выполнено, то функция следующего состояния сохранила бы свойство симметрии. Но можно легко проверить, что константы  , выбраны так, что
, выбраны так, что  . Таким образом, функция следующего состояния не подвержена атаке на основе связанного ключа.
. Таким образом, функция следующего состояния не подвержена атаке на основе связанного ключа.Атака на основе частичного угадывания ключа
Guess-and-Verify Attack
Такая атака станет возможной, если выходные биты можно будет предсказать с помощью небольшого набора битов внутреннего состояния. Злоумышленник должен отгадать соответствующую часть переменных состояния, предсказать выходные биты и сравнить их с непосредственно наблюдаемыми битами на выходе, чтобы удостовериться в правильности своей догадки. Злоумышленник должен угадать, по крайней мере, 2*12 входных байт для различных g-функций для проверки в отношении одного байта. Это равносильно угадыванию 192 битов, что сложнее, чем полный перебор всех ключей.
Guess-and-Determine Attack
Суть этого метода заключается в том, что надо угадать несколько неизвестных переменных шифра и, используя их, вывести оставшиеся неизвестные. После этого систему прогоняют несколько раз, и то что получилось на выходе сравнивают с реальным выходными данными шифра для проверки предположения. Злоумышленник пытается воссоздать 512 бит внутреннего состояния, т.е. он наблюдает 4 последовательных 128-битных данных на выходе шифра и делает следующее:
- Разделяет 32-битный счетчик и 32-битную переменную состояния на 8-битовые переменные.
- Составляет систему уравнений, которая моделирует изменение счетчиков и переменных состояния, и выходные данные. В итоге получается 160 уравнений и 160 неизвестных.
- Решает эту систему, угадывая как можно больше неизвестных.
Эффективность такого подхода зависит от количества угаданных переменных. Это количество ограниченно снизу 8-битовой подсистемой с наименьшим количеством входных переменных. Если пренебречь счетчиками, каждый байт функции следующего состояния зависит от 12 входных байт. Если учитывать счетчики, каждый байт на выходе подсистемы зависит уже от 24 входных байт. Следовательно, злоумышленник должен угадать более чем 128 бит, таким образом, делая нападение невыполнимым.
Алгебраические атаки
Алгебраически нормальная форма(АНФ) g-функции
Дана Булева функция
 , АНФ является представлением
, АНФ является представлением  как многомерного полинома(т.е. сумма одночленов от входных переменных). Большое количество одночленов и их хорошее распределение по степеням – важные свойства нелинейных блоков в шифре.
как многомерного полинома(т.е. сумма одночленов от входных переменных). Большое количество одночленов и их хорошее распределение по степеням – важные свойства нелинейных блоков в шифре.Для случайной Булевой функции в 32 переменных, среднее число одночленов равняется
 , а среднее число одночленов, включающие все данные переменные –
, а среднее число одночленов, включающие все данные переменные –  . Если мы рассмотрим 32 такие функции, выбранные случайным образом, то среднее число одночленов, которых нет ни в одной из 32 функций, равно 1, и соответствующая дисперсия также равна 1.
. Если мы рассмотрим 32 такие функции, выбранные случайным образом, то среднее число одночленов, которых нет ни в одной из 32 функций, равно 1, и соответствующая дисперсия также равна 1.Для g-функции в шифре Rabbit, АНФ для 32 булевых подфункций имеют, по крайней мере, степень 30. Число одночленов варьируется от
 до
до  , где для случайной функции оно должно быть
, где для случайной функции оно должно быть  . Распределение одночленов как функции степени представлено на рисунке. В идеале, основная часть должна была находиться промежутке между пунктирными линиями, которые показывают отклонения от среднего для идеальной случайной функции. Некоторые Булевы функции значительно расходятся с результатами для случайной функции, однако, все они имеют большое число одночленов высокой степени.
. Распределение одночленов как функции степени представлено на рисунке. В идеале, основная часть должна была находиться промежутке между пунктирными линиями, которые показывают отклонения от среднего для идеальной случайной функции. Некоторые Булевы функции значительно расходятся с результатами для случайной функции, однако, все они имеют большое число одночленов высокой степени.К тому же, исследовалось частичное совпадение 32 функций. Общее число одночленов, которые встречаются один раз, равно
 , в то время как число одночленов, которые не встречаются вовсе –
, в то время как число одночленов, которые не встречаются вовсе –  . Если сравнить со случайной функцией, то это довольно большие отклонения. Эта информация может быть полезна для анализа шифра в будущем.
. Если сравнить со случайной функцией, то это довольно большие отклонения. Эта информация может быть полезна для анализа шифра в будущем.Алгебраически нормальная форма(АНФ) для полного шифра
Практически невозможно рассчитать АНФ для всех битов на выходе для полного шифра. Но уменьшение размера ключа с 128 бит до 32 бит делает это возможным для изучения 32 булевых функций на выходе как функцию от 32 битного ключа.
Для урезанной версии шифра Rabbit, была исследована функция установки для различного числа итераций. АНФ определяется после 0, 1, 2, 3, 4 итераций и одной дополнительной в схеме извлечения. Для 0+1 итераций число одночленов было примерно равно 2^31, как предполагалось для случайной функции. Но после двух итераций результат стабилизировался. Это означает, что больше нет колебаний на выходе. Количество отсутствующих полиномов 0, 1, 2, 3, 1 в итерациях (0+1), …, (4+1) соответственно. Очевидно, что эти данные соответствуют результатам для случайных функций.
Корреляционные атаки
Линейная аппроксимация
Линейная атака подразумевает нахождение лучшего линейного приближения между битами на входе функции следующего состояния и битами на выходе схемы извлечения. Для этого используют Преобразование Уолша – Адамара, полагая, что все входные данные линейно независимы. Было установлено, что наилучшая линейная корреляция имеет коэффициент корреляции порядка
 , что подразумевает генерацию выходных данных от
, что подразумевает генерацию выходных данных от  итераций, чтобы сравнить со случайной функцией.
итераций, чтобы сравнить со случайной функцией.Аппроксимация второго порядка
Отсекание из АНФ для g-функции членов выше второго порядка значительно улучшает аппроксимацию при правильных условиях.
Обозначим через
![f^{[j]}](f01609908a4196c893e5c9454fd6cf9f.png) аппроксимацию второго порядка АНФ для
аппроксимацию второго порядка АНФ для ![g^{[j]}](846a6a4b4698af7ecbc20ef29053e2b3.png) . По результатам эксперимента коэффициент корреляции между
. По результатам эксперимента коэффициент корреляции между  и
и  составляет менее
составляет менее  , а коэффициент корреляции между
, а коэффициент корреляции между ![f^{[j]} \oplus f^{[j+1]}](b1eedebe62c6fb53fddb5e74580a2b38.png) и
и ![g^{[j]} \oplus g^{[j+1]}](9a07a7abe184ac53619a5844d43df31c.png) примерно равен
примерно равен  . Это означает, что некоторые члены более высокой степени отсекаются при сложении по модулю 2 двух соседних битов. Построение по этим данным шифра со вторым порядком аппроксимации дает, в лучшем случае, коэффициент корреляции порядка
. Это означает, что некоторые члены более высокой степени отсекаются при сложении по модулю 2 двух соседних битов. Построение по этим данным шифра со вторым порядком аппроксимации дает, в лучшем случае, коэффициент корреляции порядка  . Данное значение коэффициента корреляции является недостаточным для атаки. Если еще учитывать счетчики, то анализ намного усложняется.
. Данное значение коэффициента корреляции является недостаточным для атаки. Если еще учитывать счетчики, то анализ намного усложняется.Список литературы
- ↑ M. Boesgaard, M. Vesterager, T. Pedersen, J. Christiansen, O. Scavenius. Rabbit: A High-Performance Stream Cipher. Proc. FSE 2003. Springer LNCS 2887, pp. 307-329 (PDF)
- ↑ M. Boesgaard, T. Pedersen, M. Vesterager, E. Zenner. The Rabbit Stream Cipher - Design and Security Analysis. Proc. SASC 2004. (PDF)
- ↑ Phorum :: ECRYPT forum :: Rabbit becomes public domain
- ↑ The eSTREAM Portfolio Steve Babbage, Christophe De Canni`ere, Anne Canteaut, Carlos Cid, Henri Gilbert, Thomas Johansson, Matthew Parker, Bart Preneel, Vincent Rijmen and Matthew Robshaw6 (PDF)
- ↑ Christophe De Cannière, Joseph Lano, and Bart Preneel, "Comments on the Rediscovery of Time Memory Data Tradeoffs", 2005. (PDF)
Ссылки
Симметричные криптосистемы Поточный шифр Сеть Фейстеля ГОСТ 28147-89 • Blowfish • Camellia • CAST-128 • CAST-256 • CIPHERUNICORN-A • CIPHERUNICORN-E • CLEFIA • Cobra • DFC • DEAL • DES • DESX • EnRUPT • FEAL • FNAm2 • HPC • IDEA • KASUMI • Khufu • LOKI97 • MARS • NewDES • Raiden • RC5 • RC6 • RTEA • SEED • Sinople • TEA • Triple DES • Twofish • XTEA • XXTEA
SP-сеть Другие Категория:- Потоковые шифры
Wikimedia Foundation. 2010.

























![s^{[15..0]}_i = x^{[15..0]}_{0,i} \oplus x^{[31..16]}_{5,i}](1aaf9489893ec38b4a4dcc2e72c55659.png)
![s^{[31..16]}_ i = x^{[31..16] }_{0,i }\oplus x^{[15..0]}_{3,i}](18ae741dcba79c3d5adc2ff8e51e8ab3.png)
![s^{[47..32]}_i = x^{[15..0]}_{2,i }\oplus x^{[31..16]}_{7,i }](023f630f144c7f7a06cbb3a2de23dc0a.png)
![s^{[63..48]}_i = x^{[31..16]}_{2,i} \oplus x^{[15..0]}_{5,i}](f4dce2d21439d8d9a92da1cab8fa2d8e.png)
![s^{[79..64]}_i = x^{[15..0]}_{4,i }\oplus x^{[31..16]}_{1,i }](b0f84c4ce8882f1c4cacb6e3259e60b0.png)
![s^{[95..80]}_i = x^{[31..16]}_{4,i} \oplus x^{[15..0]}_{7,i}](9acd136f1cd7a1b2ad530ad394c462a7.png)
![s^{[111..96]}_i = x^{[15..0]}_{6,i }\oplus x^{[31..16]}_{3,i }](123a0a433fd7402f694b4b2b0c4b7f72.png)
![s^{[127..112]}_i = x^{[31..16]}_{6,i}\oplus x^{[15..0]}_{1,i}](1adb00860de14efe66be403b4c6de148.png)


