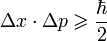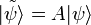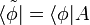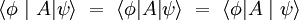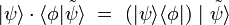Обозначения Дирака

〈	∣	〉
bra		ket
бра		кет

Квантовая механика

$\Delta x\cdot\Delta p \geqslant \frac{\hbar}{2}$

Принцип неопределённости

Введение ... Математическая формулировка ... Основа Классическая механика · Интерференция · Бра и кет · Гамильтониан Фундаментальные понятия Квантовое состояние · Волновая функция · Суперпозиция · Запутанность · Измерение · Неопределённость · Запрет Паули · Дуализм · Декогеренция · Теорема Эренфеста · Туннелирование Эксперименты Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга ·Проверка неравенств Белла · Фотоэффект · Эффект Комптона Формулировки Картина Шрёдингера · Картина Гейзенберга · Картина взаимодействия · Матричная квантовая механика · Интегралы по траекториям Уравнения Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака Интерпретации Копенгагенская интерпретация · Теория скрытых параметров · Многомировая Сложные темы Квантовая теория поля · Квантовая гравитация · Теория всего Известные учёные Планк · Эйнштейн · Шрёдингер · Гейзенберг· Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт

Бра и кет (англ. bra-ket ← bracket скобка) — алгебраический формализм (система обозначений), предназначенный для описания квантовых состояний. Называется также обозначениями Дирака. В матричной механике данная система обозначений является общепринятой.

Определение и использование

Квантовая система рассматривается в гильбертовом пространстве 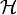$\mathcal{H}$, элементы (векторы) которого обозначаются как 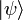$|\psi\rangle$ «кет-векторы». Сопряжённое пространство 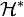$\mathcal{H}^*$, элементы которого обозначаются как 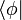$\langle \phi |$ «бра-векторы», совпадает с 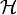$\mathcal{H}$ с точностью до комплексного сопряжения. Это означает, что каждому кет-вектору 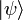$|\psi\rangle$ можно сопоставить бра-вектор 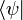$\langle \psi |$, и обратно.

Скалярное произведение бра-вектора с кет-вектором записывается в виде 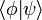$\langle \phi |\psi\rangle$; две вертикальные черты «сливаются». Квадрат вектора, по определению гильбертова пространства, неотрицателен: 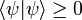$\langle \psi |\psi\rangle \ge 0$. На вектора, описывающие состояния системы, накладывается условие нормировки $\langle \psi |\psi\rangle = 1$.

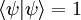Свёртка оператора А с бра-вектором 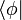$\langle \phi |$ и кет-вектором 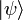$|\psi\rangle$ записывается как 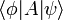$\langle \phi |A|\psi\rangle$; это также скаляр (комплексное число). В частности, матричный элемент оператора А в определённом базисе (в тензорных обозначениях — A_kl) записывается в обозначениях Дирака как 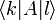$\langle k |A|l\rangle$, а среднее значение наблюдаемой на состоянии ψ — как $\langle\psi|A|\psi\rangle$.

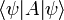Умножение векторов на оператор (кет-вектора — слева, бра-вектора — справа) даёт векторы того же типа и записывается тем же способом, что принят в алгебре:

$|\tilde\psi\rangle = A|\psi\rangle$

$\langle \tilde\phi | = \langle \phi |A$

Например, уравнение Шрёдингера (для стационарного состояния) будет иметь вид:

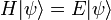$H|\psi\rangle = E|\psi\rangle$ , где H — гамильтониан, а E — скаляр (уровень энергии).

Отличия бра-кет-обозначений от традиционных

В математике употребляется обозначение «полуторалинейного» скалярного произведения 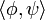$\langle \phi ,\psi\rangle$ в гильбертовом пространстве, имеющее тот же смысл, что и перемножение бра на кет. Однако, математики обычно рассматривают угловые скобки как знак операции, а не части обозначения вектора. Традиционное математическое обозначение, в отличие от дираковского, несимметрично — оба вектора предполагаются величинами одного типа, и по первому аргументу из двух операция является антилинейной. С другой стороны, произведение бра и кет является билинейным, но от двух аргументов разного типа. Сопряжённым к кет-вектору 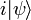$i|\psi\rangle$ будет являться бра-вектор 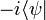$-i \langle \psi |$ (где i — мнимая единица). Однако, в квантовой механике эту странность обозначений позволено игнорировать, поскольку квантовое состояние, представляемое вектором, не зависит от его умножения на любые комплексные числа, по модулю равные единице. Также, использование бра и кет позволяет подчеркнуть отличие состояния ψ (записывается без скобок и палок) от конкретных векторов, его представляющих.

В отличие от алгебраических обозначений, где элементы базиса обозначаются как e_k, в бра-кет-обозначениях указывается только индекс базисного элемента: 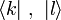$\langle k|\ ,\ |l\rangle$. Этим они похожи на тензорные обозначения, но в отличие от последних позволяют записывать произведения операторов с векторами без использования дополнительных (подстрочных или надстрочных) букв.

Математические свойства

Бра и кет можно использовать и в чистой математике для обозначения элементов сопряжённых друг другу линейных пространств. Кет-векторы считаются при этом «векторами-столбцами», а бра-векторы — «векторами-строками». Перемножение бра- и кет-векторов друг на друга и на операторы можно рассматривать как частный случай матричного формализма «строка на столбец». А именно, надо положить кет-векторы матрицами размера N×1, бра-векторы — размера 1×N, операторы — размера N×N, где N — количество состояний квантовой системы (размерность пространства 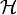$\mathcal{H}$). Матрицы размера 1×1 имеют единственный элемент и отождествляются со скалярами. В случае бесконечномерного пространства состояний на «матрицы» (фактически, ряды) приходится накладывать дополнительные условия сходимости.

Формула для сопряжённого вектора выглядит следующим образом:

$\langle \psi | = \begin{pmatrix}\overline{c_1} & \overline{c_2} & \cdots & \overline{c_N}\end{pmatrix}$

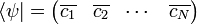
, где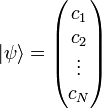

$|\psi\rangle = \begin{pmatrix} c_1 \\ c_2 \\ \vdots \\ c_N \end{pmatrix}$

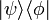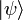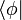Запись типа  〈 … 〉  всегда означает скаляр. Бра-вектор всегда имеет скобку  〈  слева, кет-вектор — скобку  〉  справа. Произведение в «неестественном» порядке —  〉 〈  — даёт так называемый кет-бра-оператор $|\psi\rangle \langle \phi|$ — оператор ранга 1, являющийся тензорным произведением $|\psi\rangle$ и $\langle \phi|$. Они часто рассматриваются в теории операторов и квантовых вычислениях. В частности, оператор 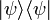$|\psi\rangle \langle \psi|$ (при нормировке 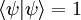$\langle \psi |\psi\rangle = 1$) является проектором на состояние ψ, точнее, на соответственное одномерное линейное подпространство в $\mathcal{H}$.

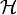Имеет место ассоциативность:

$\langle\phi\ |\ A|\psi\rangle\ =\ \langle\phi |A|\psi\rangle\ =\ \langle \phi |A\ |\ \psi\rangle$

$|\psi\rangle\cdot\langle\phi |\tilde\psi\rangle\ =\ (|\psi\rangle\langle\phi|)\ |\ \tilde\psi\rangle$

и т.д.

Интересные факты

• На семинаре в Институте физических проблем во время выступления Дирака, Ландау переводил термины "бра" и "кет" как "ско" и "бка".

Литература

• Ю. М. Белоусов. Курс квантовой механики. Нерелятивистская теория. Москва. 2006.